1장 컴퓨터 내부의 언어 체계 - 컴퓨터는 어떤 말을 사용할까
언어란 무엇인가
모든 언어의 뜻은 기호의 집합으로 인코딩된다. 의사소통하는 당사자 모두 같은 문맥을 공유해서 같은 기호에 같은 뜻�을 부여할 수 있어야 한다.
문자 언어
다음과 같은 세 가지 구성 요소가 문자 언어의 틀을 이루는데, 컴퓨터 언어에서도 마찬가지다.
- 기호가 들어갈 상자
- 상자에 들어갈 기호
- 상자의 순서
일부 언어에는 주변의 상자 안에 들어 있는 기호의 종류에 따라 상자에 들어갈 수 있는 기호를 제한하는 복잡한 규칙이 존재하기도 한다. 예를 들어, 어떤 기호들은 서로 인접한 상자에 들어갈 수 없다.
비트
자연어에서는 상자를 문자라고 부르고 컴퓨터에서는 비트라고 부른다. '비트'라는 단어는 2진법을 사용한다는 뜻의 '바이너리'와 숫자를 뜻하는 '디지트'가 합쳐진 말이다.
논리 연산
비트 사용법 중 하나는 예/아니요 질문에 대한 답을 표현하는 것이다. '예'를 참이라는 용어로 부르고, '아니요'를 거짓이라는 용어로 부른다.
다른 비트들이 표현하는 내용으로부터 새로운 비트를 만들어내는 이런 동작을 논리 연산이라고 한다.
불리언 대수
일반 대수와 마찬가지로 결합 법칙, 교환 법칙, 분배 법칙을 불리언 대수에 적용할 수 있다.
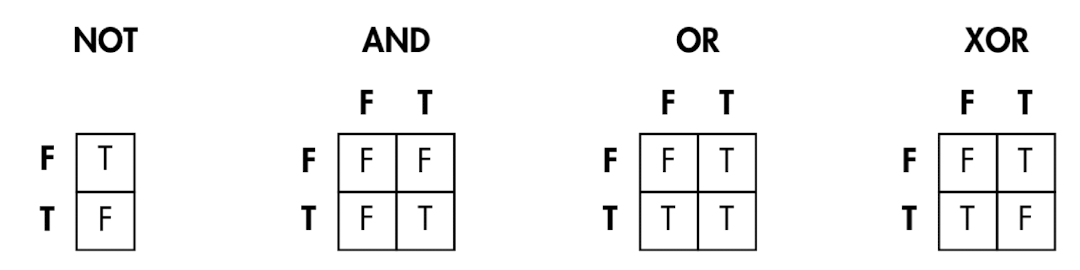
- NOT: '논리적 반대'를 의미한다.
- AND: 2비트 연산인 경우 첫 번째 비트가 참이고 두 번째 비트도 참인 경우에만 결과가 참이 된다. 2비트보다 더 많은 비트에 연산을 적용하는 경우 모든 비트가 참이면 AND 연산의 결과도 참이다.
- OR: 2비트 연산인 경우 첫 번째 비트가 참이거나 두 번째 비트가 참이면 결과가 참이 된다. 2비트보다 더 많은 비트에 연산을 적용하는 경우 어느 한 비트라도 참이면 OR 연산의 결과도 참이다.
- XOR(exclusive OR): 첫 번째 비트와 두 번째 비트가 다른 값인 경우에만 참이 된다. 즉 두 값 중 어느 하나가 참이면 XOR도 참이지만 두 값이 모두 참이면 XOR의 결과는 거짓이다.
드모르간의 법칙
a AND b 라는 연산은 NOT(NOT a OR NOT b) 와 같다고 말한다.
NOT을 사용하면 AND 연산을 OR 연산으로 대신할 수 있다. 긍정적인 논리에 더해 부정적인 논리를 기술하는 명제를 사용할 때 드모르간의 법칙을 활용할 수 있다.
정수를 비트로 표현하는 방법
양의 정수 표현
2진수 체계는 10을 밑으로 하지 않고 2를 밑으로 하는 수 체계다.
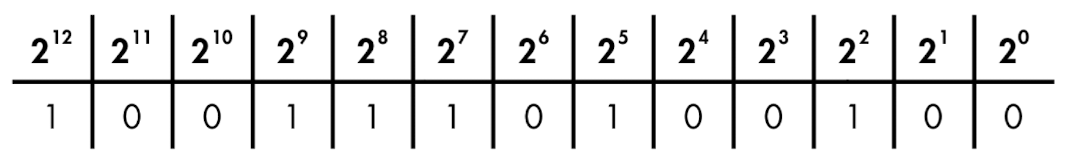
2진수의 비트 개수는 표현할 수 있는 값의 범위를 결정한다.
- 가장 작은 유효 비트(LSB, Least Significant Bit): 2진수에서 가장 오른쪽의 비트
- 가장 큰 유효 비트(MSB, Most Significant Bit): 2진수에서 가장 왼쪽의 비트
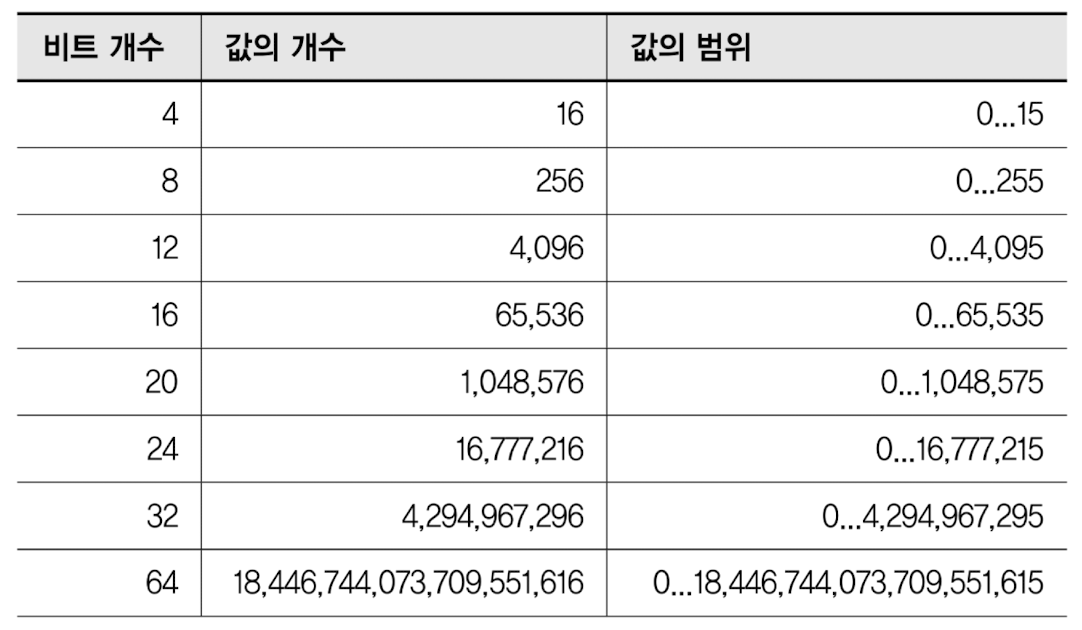
컴퓨터가 미리 정해진 수의 비트를 한 덩어리로 사용하도록 만들어졌기 때문에, 2진수를 쓸 때는 이런 식으로 항상 일정한 개수의 비트를 사용해 값을 표현하는 경우가 종종 있다.